Dynamic systems, characterized by their nonlinear nature, possess an inherent unpredictability that makes them notoriously challenging to model. From the climate and human brain to the electric grid, these complex systems undergo dramatic changes over time, often triggering significant effects elsewhere. As researchers grapple with the need to comprehend and predict these intricate behaviors, machine learning has emerged as a promising approach. In particular, reservoir computing, a simple yet powerful machine learning technique, has garnered attention for its ability to model high-dimensional chaotic behaviors effectively. However, a recent study by Yuanzhao Zhang and physicist Sean Cornelius sheds light on previously overlooked limitations within reservoir computing, highlighting the intricacies and challenges that impede its widespread implementation.
Reservoir computing, an approach proposed by computer scientists over two decades ago, has proven to be a nimble and cost-effective predictive model compared to other neural network frameworks. By leveraging neural networks, reservoir computing captures the complex dynamics of a system without the need for an explicit mathematical description. Its simplicity and ability to perform with minimal training data make it an appealing option for modeling various dynamic systems. In 2021, researchers introduced the next-generation reservoir computing (NGRC), which presents several advantages over conventional reservoir computing, including reduced data requirements for training.
Zhang and Cornelius embarked on an investigation of both standard reservoir computing and NGRC, aiming to identify their limitations in modeling dynamic systems accurately. Their findings revealed specific shortcomings that hinder the applicability of these techniques, thereby emphasizing the need for further research and development.
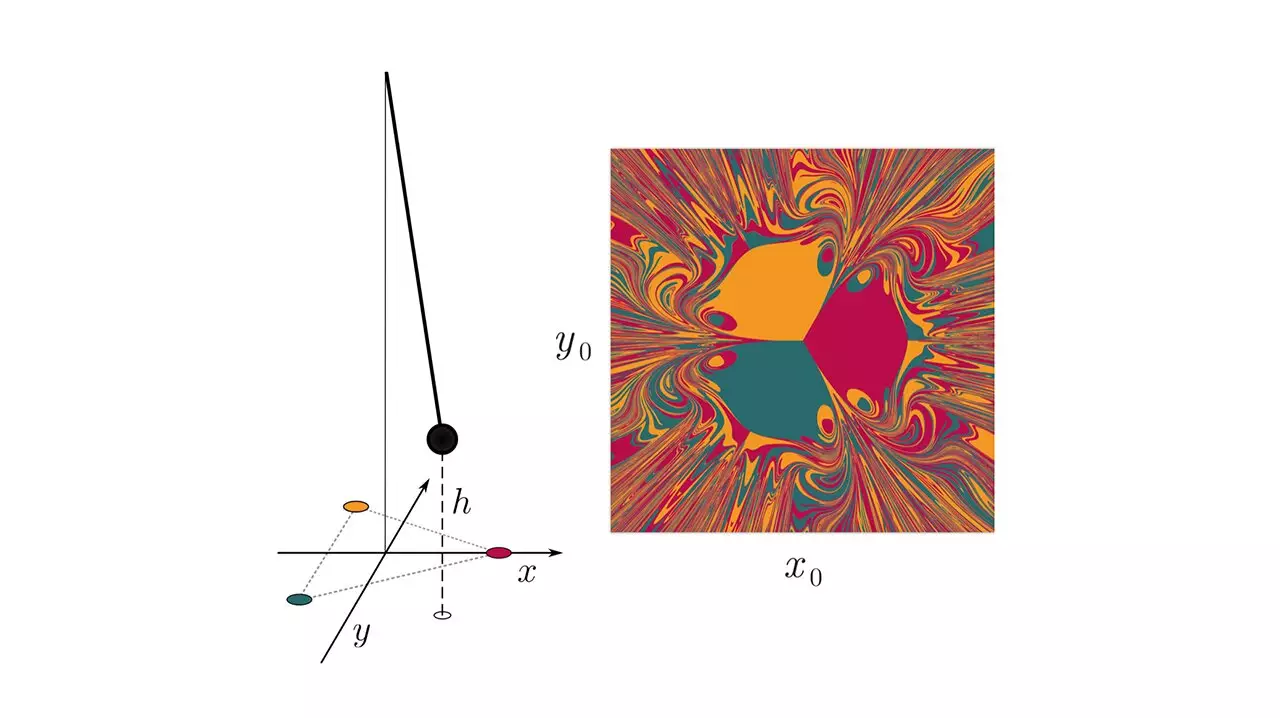
In the case of NGRC, the researchers examined a simple dynamic chaotic system involving a pendulum with a magnet attached, swinging amidst three fixed magnets arranged in a triangular pattern. They discovered that if the system was provided information about the required nonlinearity to describe its behavior, the NGRC model performed admirably. However, when the model was perturbed or subjected to unexpected changes, its performance significantly deteriorated. This indicates that accurate predictions using NGRC heavily rely on pre-existing knowledge about the system, limiting its flexibility in unpredictable situations.
On the other hand, standard reservoir computing exhibited a distinct issue. The researchers observed that for the model to accurately predict the system’s behavior, it required a lengthy “warm-up” period equivalent to the dynamic movements of the magnet itself. This demand for extensive warm-up time poses a considerable challenge, especially when dealing with complex and rapidly evolving dynamic systems. The time-consuming nature of the warm-up phase may outweigh the supposed advantages of reservoir computing, rendering it impractical in certain scenarios.
Acknowledging the limitations of both reservoir computing and NGRC is the first step towards harnessing their full potential in modeling dynamic systems. Yuanzhao Zhang emphasizes the importance of addressing these challenges to improve the applicability of this emerging computing framework. By developing strategies to overcome the Catch-22 problems associated with reservoir computing, researchers can unlock new possibilities and make meaningful advancements in understanding, predicting, and controlling complex dynamic systems.
Reservoir computing has shown promise as a machine learning approach for modeling dynamic systems. However, an in-depth analysis conducted by Zhang and Cornelius has exposed critical limitations that hinder its widespread use. The reliance on pre-existing knowledge and the significant warm-up time required for accurate predictions present challenges that must be addressed for reservoir computing to reach its full potential. Nevertheless, by recognizing these limitations and actively working to overcome them, researchers can pave the way for more effective and reliable modeling techniques in the realm of dynamic systems. With continued advancements in machine learning and a deeper understanding of complex behaviors, the intricate web of dynamic systems may gradually unravel before our eyes.


Leave a Reply