In the evolving landscape of quantum computing, understanding the dynamics of quantum systems through simulations is crucial. Quantum simulations provide researchers with the ability to model complex particle behaviors that are intractable through classical computational methods. Traditionally, Hamiltonians—mathematical representations of energy in a quantum system—have posed challenges in accurately estimating their parameters in experimental setups. A recent collaborative effort across various institutions, including Freie Universität Berlin and Google AI, aims to address these challenges by developing refined techniques for estimating Hamiltonian parameters in superconducting quantum simulators.
The journey for the researchers, led by Jens Eisert, began with an urgent call from friends involved with Google AI during a conference in Brazil. They faced significant hurdles while calibrating their Sycamore quantum chip. Initially, the problem appeared straightforward; however, Eisert quickly encountered complexities. He gathered a talented team of Ph.D. students, realizing that achieving precise Hamiltonian identification would take time and multiple iterations of experimentation. The project grew in scope, as overcoming the limitations presented by real-world data required innovative thinking and robust methodologies.
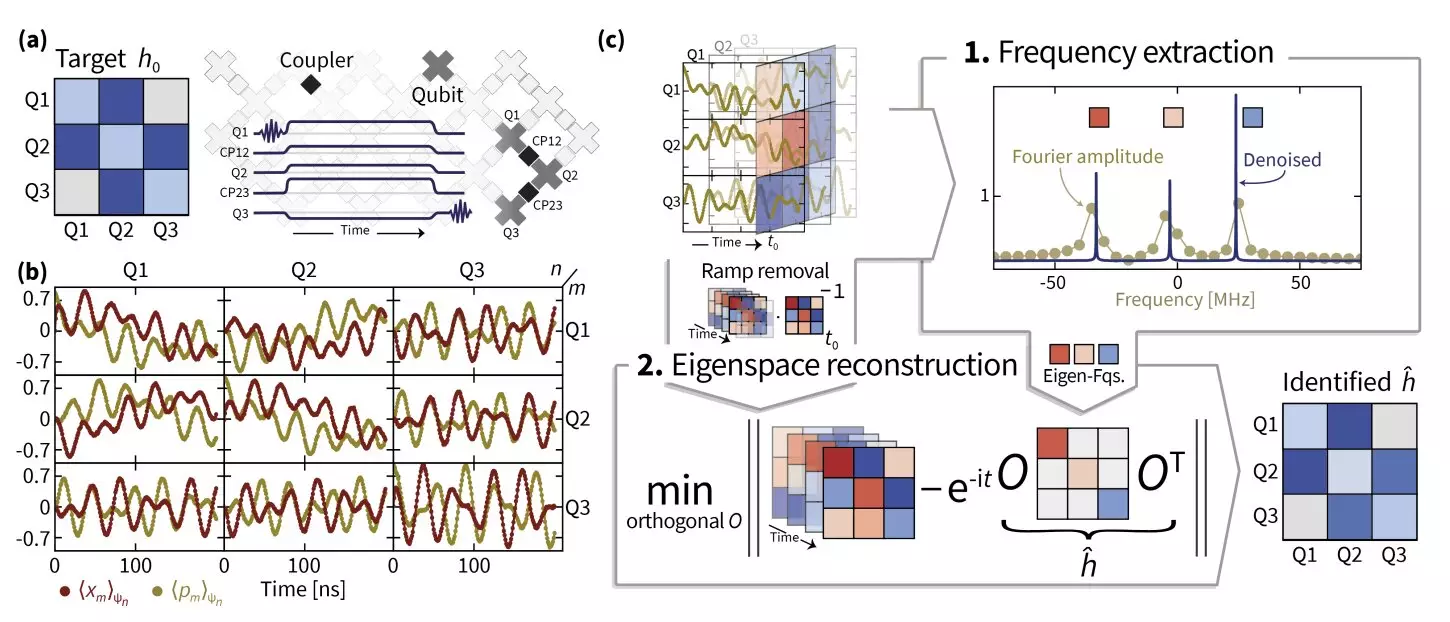
Eisert and his team embraced multi-faceted strategies to unravel the intricacies of Hamiltonian dynamics. They implemented superresolution techniques, which enhance eigenvalue estimations, thereby refining the identification of Hamiltonian frequencies. Central to their approach was a method known as manifold optimization. This technique allows researchers to navigate complex variable interactions on curved spaces instead of the flat landscapes of traditional Euclidean geometry. Through manifold optimization, the researchers could recover the eigenspaces of Hamiltonian operators and ultimately reconstruct the entire Hamiltonian itself.
As abstract as these techniques may sound, the practicalities of Hamiltonian learning imposed real-world complications. Eisert highlighted that understanding the non-idealities in switching processes—how systems turn on and off—was essential. Imperfections in these transitions could skew results. The team’s iterative learning led to the inception of their novel technique, TensorEsprit, which enhanced signal processing capabilities, proving critical for large-scale systems.
The emergence of TensorEsprit represents a pivotal moment in the field of quantum physics and computational analysis. By integrating this super-resolution approach with existing optimization frameworks, the researchers successfully identified Hamiltonian parameters in superconducting qubits, comprising up to 14 coupled quantum bits spread across two Sycamore processors. Throughout the process, the meticulous attention to eigenvalue precision was underscored as being foundational for meaningful recovery of eigenspaces.
However, the journey was not devoid of challenges. Eisert noted a scarcity of existing literature on Hamiltonian learning due to the inherently difficult nature of working with practical data. Despite these challenges, the researchers’ early results indicates a promising scalability of their methods, paving the way for broader applicability in quantum processing contexts.
The horizon for this research is vast and inspiring, with Eisert and his colleagues eager to extend their work into more interactive quantum systems and beyond. Notably, they are looking to blend their innovations with concepts from tensor networks, particularly in the study of cold atom quantum systems—a domain pioneered by physicist Immanuel Bloch. Such explorations hold the potential for a deeper understanding of Hamiltonians, catalyzing quantum simulations with unprecedented precision.
Ultimately, the crux of this research lies in the fundamental queries regarding the nature of Hamiltonians themselves. While often simplified in theoretical discussions, the real challenges emerge when it comes to practical applications and experimental results. The researchers argue that gaining precise knowledge of Hamiltonians is critical for predicting behaviors in quantum systems. Their ongoing endeavors not only aim to refine quantum technologies but provide a foundational understanding that could reshape the future of quantum simulations and, more broadly, quantum physics. The successful characterization of analog quantum simulators could significantly revolutionize how complex quantum systems and materials are studied, unlocking new avenues for scientific discovery in laboratory settings.

Leave a Reply